FRACTIONS OF WHOLES
Up
Pythabacus Facebook
Games And Activities
Pythabacus Simulation
Polygonal Numbers
Pythagorean Theorem
Primary Multiplication
Primary Addition
Subtraction
Counting
Numerals
Simple Times Lesson
Simple Plus Lesson
Simple Minus Lesson
Short Multiplication
Short Division
Fractions
Reducing Fractions
Fractions Of Wholes
Multiplying Fractions
Division Of Fractions
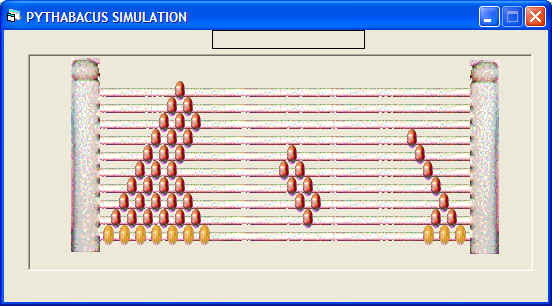
Pythabacus Videos		 Once students can divide on the Pythabacus then they can explore multiplying a whole number by a fraction.  For the example two-thirds (times or of) twelve, tell the students a family of three squirrels collected twelve nuts and each took one nut in turn from the collection until  there were no nuts left. How many nuts does each squirrel get? The number of squirrels is represented by the triangle with three beads in its' base, and the collected nuts by the rectangle of beads above the triangle. 

To direct the solution process for two-thirds (of or times) twelve ask how many nuts would two of the squirrels get altogether. If you push two-thirds of the base beads of the triangle representing the family of squirrels to the left you will separate out two-thirds of the rectangle representing the collected nuts. In this way, the answer eight is displayed.              PLACE MOUSE OVER PICTURE