DIVISION OF FRACTIONS
Up
Pythabacus Facebook
Games And Activities
Pythabacus Simulation
Polygonal Numbers
Pythagorean Theorem
Primary Multiplication
Primary Addition
Subtraction
Counting
Numerals
Simple Times Lesson
Simple Plus Lesson
Simple Minus Lesson
Short Multiplication
Short Division
Fractions
Reducing Fractions
Fractions Of Wholes
Multiplying Fractions
Division Of Fractions
Pythabacus Videos

Division of fractions can be shown to be a comparison of one fraction to another. The solution process can be directed by continuing our poem.

I invited my friend again for pie.
Have no fear this is why;
I baked this time two with pride.
I ate most of one but no need to cry.
Here's another for my friend to try.
Eat my friend; do not be shy.

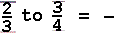Place Mouse Arrow Over Pictures To See Animation
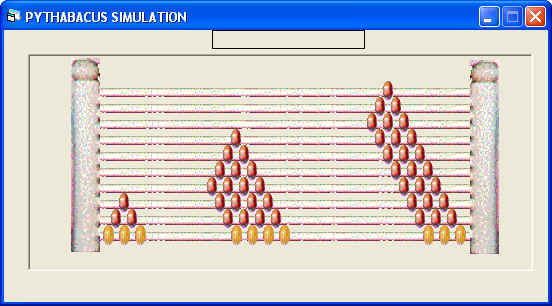
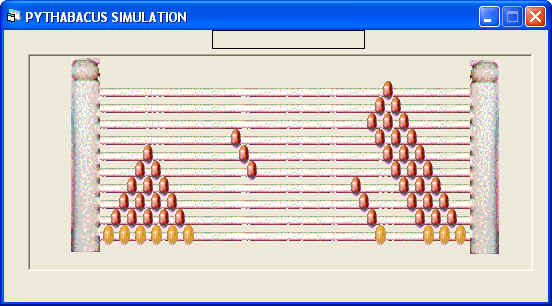
Have the students, as for multiplication of fractions, multiply the denominators to see into how many equal pieces the pie is sliced, but position the quadrilateral of beads between the separated triangles. Push 3 bottom beads against the left post to represent the denominator of 2/3. Next push 4 more bottom beads midway to the left post, then back to the right almost touching the array remaining against the right post to represent the denominator of 3/4. There will be a quadrilateral array of 12 brown beads left in the middle.

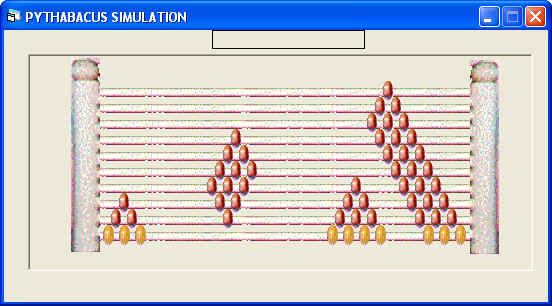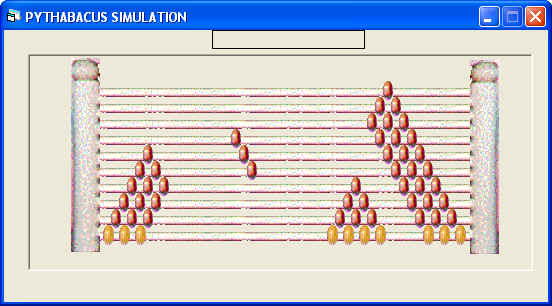
Next  have students multiply the second fraction times twelve, the product of the denominators to find the denominator of the solution. First, to represent the numerator of 3/4 push 3 of the 4 bottom beads of the 3/4 array to the left, against the 3 beads of the 2/3 array by the left post. Push these 3 beads back to the right to rejoin the 1 remaining to the right. A quadrilateral of 9 brown beads will remain touching the triangle above the 3 beads by the left post.  This fraction of beads is represented to students as the slices eaten of the first pie and is the denominator of the solution fraction. Have students write it under the solution fraction bar

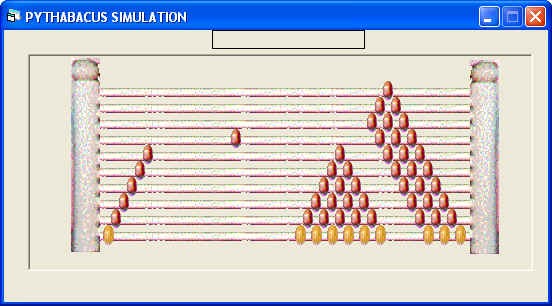
 Now have students multiply the first fraction times twelve, the product of the denominators and slices in a whole pie. To represent the numerator of 2/3 push 2 of the 3 bottom beads, by the left post, to the right until they touch the 4 beads of 3/4. When you push these 2 beads back to the left 8 brown beads will remain touching the triangle above the 4 beads of the 3/4 array representing the numerator of the solution. This fraction of beads is represented to the students as the slices eaten of the second pie by the friend and is the numerator of the solution fraction. Have student write it over the solution fraction bar. Therefore 2/3 | 3/4 = 8/9. 

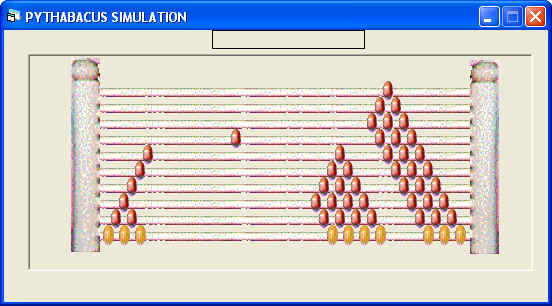
This process shows to the students that a part (two-thirds) of a whole, the second pie, is compared to a part (three-fourths) of a whole, the first pie to find the answer when dividing fractions. As for multiplication, after solving a number of division problems on the Pythabacus students may be guided to discover the numerical rule for dividing fractions.
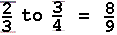